Permutation Testing

Permutation Testing

The main idea behind the cluster-permutation test as it is implemented in BESA Statistics is that if a statistical effect is found over an extended time period in several neighboring channels, it is unlikely that this effect occurred by chance.

Thus, the initial step is to define data clusters that show pronounced effects in the preliminary parametric tests.

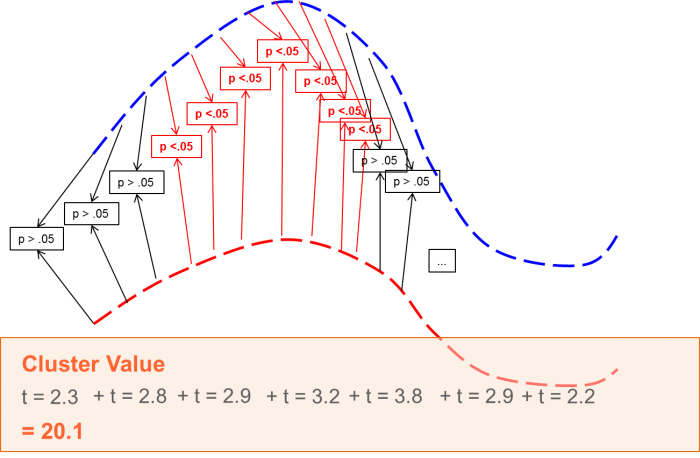
For each cluster, a cluster value can be derived consisting of the sum of all t-values / F-values of all data points in the cluster.

The null-hypothesis behind any kind of permutation test is the exchangeability of data (see also: http://www.fieldtriptoolbox.org/faq/how_not_to_interpret_results_from_a_cluster-based_permutation_test). For t-test and ANOVA / ANCOVA, the null-hypothesis assumes that the data of the input groups / conditions are exchangeable. For correlation it is assumed that the assignment of the covariate per person is random and exchangeable. In other words, the null-hypothesis in permutation testing assumes that the initial cluster values derived by the preliminary parametric test in the recorded data are as likely as cluster values derived in each permutation step.

Permutation means that the data of subjects (for unpaired t-tests, between-group ANOVA / ANCOVAs and correlations) or conditions (for paired t-tests or within-group ANOVA / ANCOVAs) get systematically interchanged. For each permutation step, new clusters and their according cluster values are determined. A distribution of all cluster values from all permutation steps will be generated from the input data.

Based on this distribution, the α-error of the initial cluster value can be directly determined. For example, if only 2% of all cluster values are larger than the initial cluster value, it can be assumed that the data of groups / conditions are not interchangeable with a chance of 98%. Therefore, the cluster is associated with the p-value 0.02 (one-sided test).

Based on the computed cluster-value distribution, the probability of each initial cluster can be directly determined.

Cross-Subject Statistics based on Permutation Tests

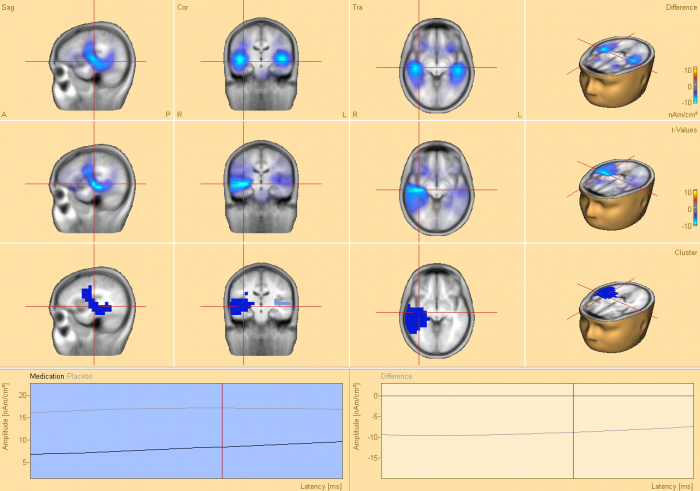
• BESA® Statistics will determine clusters in time and if applicable space and frequency where groups / conditions are not interchangeable
• The probability of the clusters will be directly determined by permutation testing
• Results are corrected for multiple comparisons